在物理学中，有一种不太常被提及但非常有趣的观点：将物理问题看作优化问题。本文将通过一个简单的例子，向大家介绍如何用梯度下降来寻找物理系统中的"最小作用路径"。这种方法不仅直观易懂，还为我们理解复杂物理现象提供了新的视角。

导语
我们通常认为物理学是关于方程和公式的科学，但实际上，它也可以被看作是一种优化过程。例如，自然界总是倾向于选择"最省力"的路径。这种思想可以用"作用量"（Action）的概念来描述：通过最小化作用量，我们可以找到物理系统的真实运动轨迹。本文将带你了解如何用现代机器学习工具——梯度下降，来解决这一经典物理问题。

标准方法回顾
在深入探讨我们的新方法之前，先来看看传统的两种解法：解析法和数值法。
解析法
解析法是我们在大学物理课上学到的经典方法。通过代数、微积分等数学工具，我们可以直接推导出系统的运动方程。例如，对于自由落体问题，其运动方程为：

下面是实现该方程的Python代码：

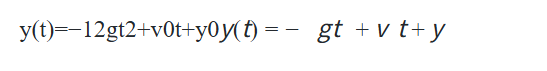
deffalling_object_analytical(x0, x1, dt, g=1, steps=100):
    v0 = (x1 - x0) / dt
    t = np.linspace(0, steps, steps+1) * dt
    x = -.5*g*t**2 + v0*t + x0  # the equation of motion
return t, x

x0, x1 = [0, 2]
dt = 0.19
t_ana, x_ana = falling_object_analytical(x0, x1, dt)

运行结果如下图所示：

数值法
并非所有物理问题都能用解析法求解。例如双摆或三体问题，它们的动力学虽然确定，但由于混沌特性，我们无法直接预测未来的状态。这时，我们需要用数值积分的方法逐步模拟系统的行为。以下是自由落体问题的数值解法：

deffalling_object_numerical(x0, x1, dt, g=1, steps=100):
    xs = [x0, x1]
    ts = [0, dt]
    v = (x1 - x0) / dt
    x = xs[-1]
for i inrange(steps-1):
        v += -g*dt
        x += v*dt
        xs.append(x)
        ts.append(ts[-1]+dt)
return np.asarray(ts), np.asarray(xs)

t_num, x_num = falling_object_numerical(x0, x1, dt)

运行结果如下图所示：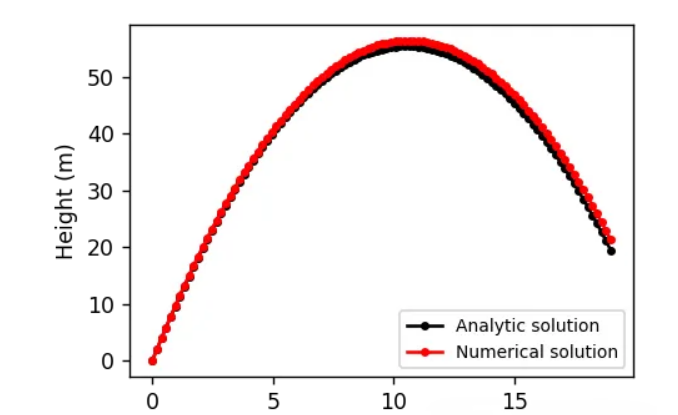

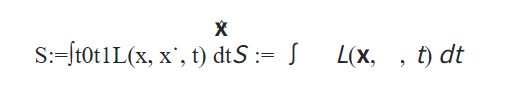
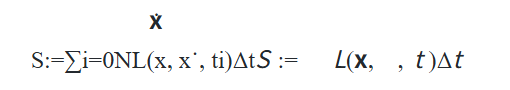
我们的方法：作用量最小化
除了上述两种传统方法，还有一种完全不同的思路：拉格朗日方法（Lagrangian Method）。这种方法的核心思想是通过最小化作用量来确定系统的运动轨迹。

拉格朗日方法的工作原理
拉格朗日方法首先考虑系统从初始状态 x(t0)x(t 0) 到最终状态 x(t1)x(t 1 ) 的所有可能路径。然后，它提供了一个简单的规则：真实路径 x^ 必须使得作用量 SS 在该路径上达到稳定值。作用量 SS 的定义如下：

其中 L=T−VL=T−V，TT 和 VV 分别表示系统的动能和势能。
为了找到真实路径 x^  ，传统方法会使用欧拉-拉格朗日方程（Euler-Lagrange Equation），这是一个偏微分方程组。通过求解这些方程，我们可以得到系统的运动轨迹。

用梯度下降寻找最小作用路径
然而，我们今天要尝试一种更直接的方法：通过梯度下降直接最小化作用量 SS。具体步骤如下：
1.将时间区间 [t0,t1][t,t ] 划分为 NN 个离散的时间点。
2.使用有限差分法近似计算速度 x˙ 。
3.定义离散化的作用量 SS 为：

使用自动微分工具（如 PyTorch）计算梯度 ∂S∂x ，并通过梯度下降算法最小化 SS。
简单实现
下面是一个用 Python 实现的简单例子：

import torch

deflagrangian_freebody(x, xdot, m=1, g=1):
    T = .5 * m * xdot**2
    V = m * g * x
return T - V

defaction(x, dt):
    xdot = (x[1:] - x[:-1]) / dt
    xdot = torch.cat([xdot, xdot[-1:]], axis=0)
    L = lagrangian_freebody(x, xdot)
return torch.sum(L) * dt

# 初始化位置坐标
x = torch.tensor([0.0] * 101, requires_grad=True)
dt = 0.19
# 堆代码网 duidaima.com
# 梯度下降优化
optimizer = torch.optim.Adam([x], lr=0.1)
for step inrange(1000):
    optimizer.zero_grad()
    S = action(x, dt)
    S.backward()
    optimizer.step()

print("Optimized positions:", x.detach().numpy())

总结与思考
本文介绍了如何用梯度下降方法寻找物理系统的最小作用路径。这种方法不仅直观，还能轻松扩展到更复杂的系统（如理想气体或多体问题）。虽然梯度下降的计算效率可能不如传统方法，但它为我们提供了一种全新的视角来理解物理规律。你是否也觉得这种方法很有趣？不妨试着将其应用到其他物理问题中，看看会有怎样的发现！