什么是红黑树？
红黑树是一种自平衡的二叉查找树，是一种高效的查找树。它是由 Rudolf Bayer 于1972年发明，在当时被称为对称二叉 B 树(symmetric binary B-trees)。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。红黑树具有良好的效率，它可在 O (logN) 时间内完成查找、增加、删除等操作。因此，红黑树在业界应用很广泛，比如 Java 中的 TreeMap，JDK 1.8中的 HashMap、C++ STL 中的 map 均是基于红黑树结构实现的。

简单介绍一下什么是O(logN)
当我们谈论算法的效率时，我们通常使用时间复杂度来描述算法的运行时间与输入规模之间的关系。时间复杂度以大O符号（O）表示。

时间复杂度 O(logN)
在时间复杂度中，O(logN) 是一种非常高效的情况。它表示算法的运行时间与输入规模的对数成正比。这意味着随着输入规模的增加，算法的运行时间将以对数的速度增长。

具体来说，假设一个算法的时间复杂度是 O(logN)，其中 N 代表输入规模。当 N 增加时，该算法的运行时间将以对数的速度增加。这意味着随着输入规模的翻倍，该算法的运行时间仅会略微增加。

O(logN) 的高效性来自于对数函数的特性。对数函数具有一个很快的增长速度，但在开始时增长很快，随着输入的增加，增长速度逐渐减缓。这使得算法能够在处理大规模输入时保持相对较低的运行时间。

红黑树的基本概念（应付面试官）
红黑树是一种特殊的二叉查找树，它除了满足二叉查找树的基本性质外，还具有以下几个特点：
1.每个节点都有一个颜色属性，要么是红色，要么是黑色。
2.根节点的颜色是黑色。
3.所有叶子节点（NIL节点）的颜色都是黑色。
4.如果一个节点是红色，那么它的两个子节点都是黑色。

5.从任意一个节点到其所有后代叶子节点的简单路径上，包含相同数量的黑色节点。

这些性质保证了红黑树在插入和删除操作后能够自动调整，使得树保持平衡状态。平衡状态指的是从根节点到叶子节点的最长路径不超过最短路径的两倍。这样就避免了二叉查找树在极端情况下退化成链表，导致效率降低。

红黑树的性质
为了方便分析，我们定义以下几个概念：
黑高（black-height）：从某个节点出发（不包括该节点）到达一个叶子节点的任意一条路径上，黑色节点的个数称为该节点的黑高，记为 bh(x)。
红黑性质（red-black property）：指红黑树满足上述五个性质。

红黑树（red-black tree）：一棵满足红黑性质的二叉查找树。

有了这些定义，我们可以推导出以下几个重要的性质：
性质1：一棵有 n 个内部节点（非 NIL 节点）的红黑树，其高度 h 不超过 2log(n+1)。证明：设 x 是红黑树中任意一个内部节点，h(x) 是以 x 为根的子树的高度，n(x) 是以 x 为根的子树内部节点的个数。由于 x 的两个子节点至少有一个是黑色（性质4），所以 h(x) >= bh(x)。另一方面，由于从 x 到其后代叶子节点的任意路径上至少有一半是黑色（性质5），所以 bh(x) >= h(x)/2。综合起来，有 h(x) >= bh(x) >= h(x)/2。由此可得 h(x) <= 2bh(x)。对于整棵树而言，设其高度为 h，内部节点个数为 n，则有 h <= 2bh(root)。由于 root 是黑色（性质2），所以 bh(root) >= 1。同时，由于每条从 root 到叶子节点路径上至少包含 bh(root) 个黑色节点，所以 n >= 2^bh(root) - 1。综合起来，有 h <= 2bh(root) <= 2log(n+1)。
性质2：在一棵红黑树中，从根节点到叶子节点的所有路径中，最长的路径不超过最短路径的两倍。证明：设 h 是红黑树的高度，bh 是红黑树的黑高。由于最短路径上全部是黑色节点，所以最短路径长度为 bh。由于最长路径上红色节点和黑色节点交替出现（性质4），所以最长路径长度为 2bh。因此，最长路径长度不超过最短路径长度的两倍。

性质3：对于一棵有 n 个内部节点的红黑树，其黑高 bh 满足不等式 bh >= log(n+1)/2。证明：由性质1可得 h <= 2log(n+1)，又由于 h >= bh，所以 bh <= log(n+1)/2。红黑树的操作

红黑树的操作
红黑树的基本操作包括查找、插入和删除。查找操作和普通的二叉查找树一样，不需要特殊处理。插入和删除操作则需要考虑如何维护红黑性质，避免树失去平衡。为了实现这一目的，我们需要使用两种基本操作：颜色变换和旋转。

颜色变换
颜色变换是指将某个节点的颜色从红色变为黑色，或者从黑色变为红色。这个操作很简单，只需要修改节点的颜色属性即可。但是，颜色变换会影响红黑性质，尤其是性质4和性质5。因此，在进行颜色变换时，需要注意以下几点：
1.颜色变换不能作用于根节点，否则会违反性质2（根是黑色）。
2.颜色变换不能作用于 NIL 节点，否则会违反性质3（所有叶子都是黑色）。
3.颜色变换不能使一个节点从红色变为红色，或者从黑色变为黑色，否则没有意义。

4.颜色变换不能使一个节点和其父节点或子节点同为红色，否则会违反性质4（每个红色节点必须有两个黑色的子节点）。

旋转
旋转是指将某个节点沿着其父子关系向上或向下移动的操作。旋转分为左旋和右旋两种，左旋是将某个节点向上提升为其右孩子的父亲，右旋是将某个节点向下降低为其左孩子的孩子。旋转操作可以保持二叉查找树的性质不变，但会改变树的形状和高度。旋转操作可以用来调整树的平衡状态，使之更加接近理想的情况。

下图展示了左旋和右旋的示意图：

左旋操作可以描述如下：
设 x 是要进行左旋的节点，y 是 x 的右孩子。
将 y 的左孩子设为 x 的右孩子，并将 y 的左孩子的父亲设为 x。
将 x 的父亲设为 y 的父亲，并更新 y 的父亲的相应孩子指针。
将 y 的左孩子设为 x，并将 x 的父亲设为 y。
右旋操作与左旋类似。

红黑树的插入
红黑树的插入操作是在二叉查找树的基础上进行的，即先按照二叉查找树的规则找到合适的位置插入新节点，然后再调整树的结构和颜色，使之恢复红黑性质。插入操作的具体步骤如下：
1.创建一个新节点 z，并将其颜色设为红色。
2.按照二叉查找树的规则，将 z 插入到合适的位置，并将其父节点设为 y。
3.如果 y 是 NIL 或者黑色，那么不需要做任何调整，直接返回。

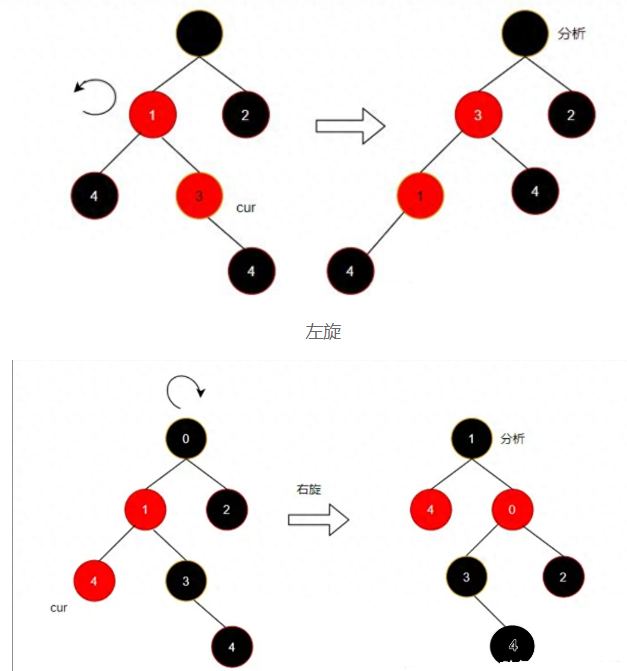
4.如果 y 是红色，那么就存在双红问题，即 z 和 y 都是红色，违反了性质4。此时，需要根据 y 的叔叔节点（y 的父节点的兄弟节点）的颜色进行不同的处理：如果 y 的叔叔节点是红色，那么将 y 和其叔叔节点的颜色都变为黑色，将 y 的父节点的颜色变为红色，并将 y 的父节点作为新的 z 节点，继续向上调整。如果 y 的叔叔节点是黑色或 NIL，那么需要进行旋转操作。具体来说，分为以下四种情况：如果 z 是 y 的右孩子，并且 y 是其父节点的左孩子，那么对 y 进行左旋，然后交换 z 和 y 的角色。如果 z 是 y 的左孩子，并且 y 是其父节点的右孩子，那么对 y 进行右旋，然后交换 z 和 y 的角色。如果 z 是 y 的左孩子，并且 y 是其父节点的左孩子，那么对 y 的父节点进行右旋，然后将 y 的颜色变为黑色，将 y 的父节点（原来的祖父节点）的颜色变为红色，并结束调整。如果 z 是 y 的右孩子，并且 y 是其父节点的右孩子，那么对 y 的父节点进行左旋，然后将 y 的颜色变为黑色，将 y 的父节点（原来的祖父节点）的颜色变为红色，并结束调整。

下图展示了插入操作的示意图：

红黑树的删除
红黑树的删除操作也是在二叉查找树的基础上进行的，即先按照二叉查找树的规则找到要删除的节点，并用其后继节点或前驱节点替换它（如果存在），然后再调整树的结构和颜色，使之恢复红黑性质。删除操作的具体步骤如下：
1.找到要删除的节点 z，并用其后继节点或前驱节点（如果存在）替换它。设替换后的新节点为 x。
2.如果 x 和 z 中至少有一个是红色，那么不需要做任何调整，直接返回。

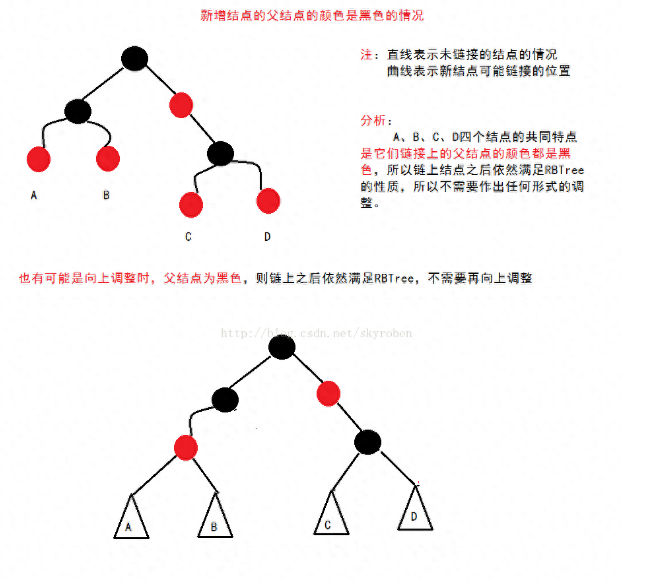
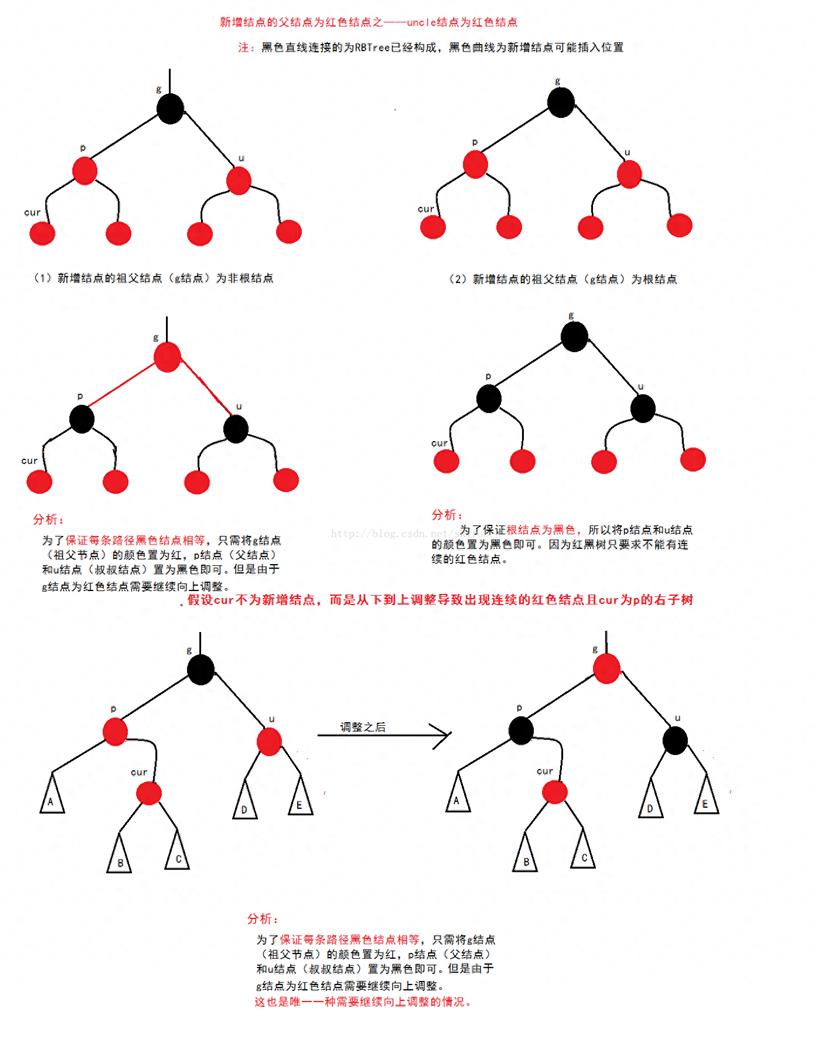
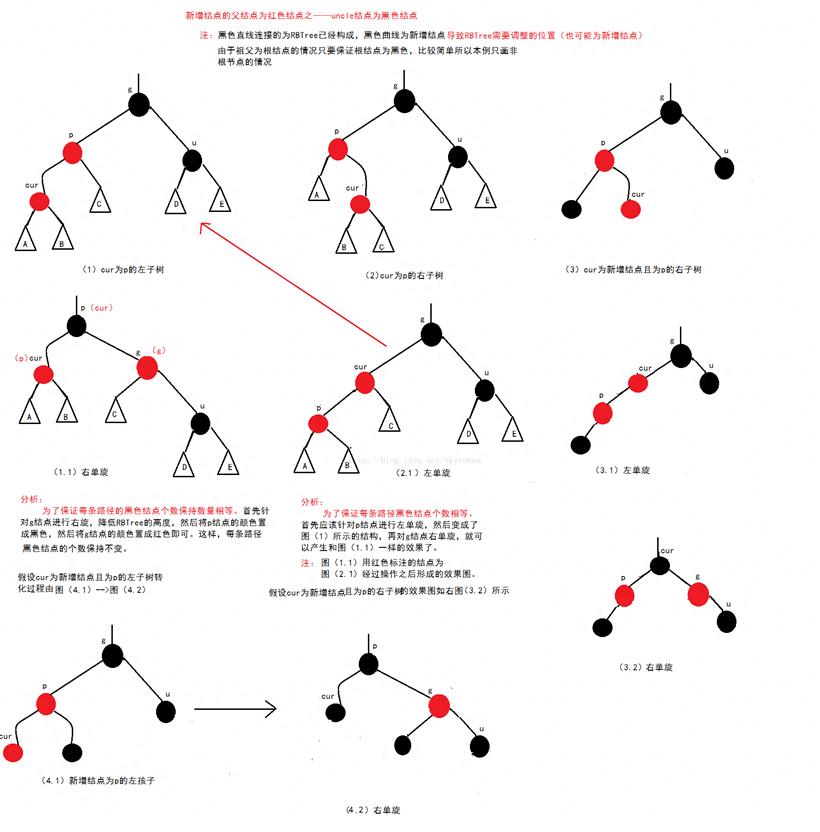
3.如果 x 和 z 都是黑色，那么就存在过度黑问题，即 x 多了一个额外的黑色属性（因为替换了 z），导致违反了性质5。此时，需要根据 x 的兄弟节点（x 的父节点的另一个孩子）的颜色进行不同的处理：如果 x 的兄弟节点是红色，那么将 x 的兄弟节点的颜色变为黑色，将 x 的父节点的颜色变为红色，并对 x 的父节点进行左旋（如果 x 是左孩子）或右旋（如果 x 是右孩子），然后更新 x 的兄弟节点。如果 x 的兄弟节点是黑色，那么分为以下四种情况：如果 x 的兄弟节点的两个孩子都是黑色或 NIL，那么将 x 的兄弟节点的颜色变为红色，并将 x 的父节点作为新的 x 节点，继续向上调整。如果 x 是左孩子，并且 x 的兄弟节点的左孩子是红色，右孩子是黑色或 NIL，那么将 x 的兄弟节点的颜色变为红色，将 x 的兄弟节点的左孩子的颜色变为黑色，并对 x 的兄弟节点进行右旋，然后更新 x 的兄弟节点。如果 x 是右孩子，并且 x 的兄弟节点的右孩子是红色，左孩子是黑色或 NIL，那么将 x 的兄弟节点的颜色变为红色，将 x 的兄弟节点的右孩子的颜色变为黑色，并对 x 的兄弟节点进行左旋，然后更新 x 的兄弟节点。如果 x 是左孩子，并且 x 的兄弟节点的右孩子是红色，那么将 x 的父节点的颜色赋给 x 的兄弟节点，将 x 的父节点和 x 的兄弟节点的右孩子的颜色都变为黑色，并对 x 的父节点进行左旋，然后结束调整。如果 x 是右孩子，并且 x 的兄弟节点的左孩子是红色，那么将 x 的父节点的颜色赋给 x 的兄弟节点，将 x 的父节点和 x 的兄弟节点的左孩子的颜色都变为黑色，并对 x 的父节点进行右旋，然后结束调整。

红黑树的实现
下面给出了用 java语言实现红黑树的部分代码。首先定义了一个 Node 类，表示树中的每个节点。每个节点有五个属性：key（键值），color（颜色），left（左孩子），right（右孩子）和 parent（父亲）。其中 color 用 0 表示黑色，用 1 表示红色。NIL 节点用 None 表示。

// 堆代码 duidaima.com
// 定义一个 Node 类，表示树中的每个节点
class Node {
    int key; // 键值
    int color; // 颜色，0 表示黑色，1 表示红色
    Node left; // 左孩子
    Node right; // 右孩子
    Node parent; // 父亲

    // 构造方法，初始化键值和颜色
    public Node(int key, int color) {
        this.key = key;
        this.color = color;
        this.left = null;
        this.right = null;
        this.parent = null;
    }
}

// 定义一个 RBTree 类，表示一棵红黑树
class RBTree {
    Node root; // 根节点

    // 构造方法，初始化根节点为 null
    public RBTree() {
        this.root = null;
    }

    // 辅助方法，对某个节点进行左旋操作
    public void leftRotate(Node x) {
        // 设 y 是 x 的右孩子
        Node y = x.right;
        // 将 y 的左孩子设为 x 的右孩子，并将 y 的左孩子的父亲设为 x
        x.right = y.left;
        if (y.left != null) {
            y.left.parent = x;
        }
        // 将 x 的父亲设为 y 的父亲，并更新 y 的父亲的相应孩子指针
        y.parent = x.parent;
        if (x.parent == null) { // 如果 x 是根节点，那么将 y 设为新的根节点
            this.root = y;
        } else if (x == x.parent.left) { // 如果 x 是其父节点的左孩子，那么将 y 设为其父节点的左孩子
            x.parent.left = y;
        } else { // 如果 x 是其父节点的右孩子，那么将 y 设为其父节点的右孩子
            x.parent.right = y;
        }
        // 将 y 的左孩子设为 x，并将 x 的父亲设为 y
        y.left = x;
        x.parent = y;
    }

    // 辅助方法，对某个节点进行右旋操作
    public void rightRotate(Node x) {
        // 设 y 是 x 的左孩子
        Node y = x.left;
        // 将 y 的右孩子设为 x 的左孩子，并将 y 的右孩子的父亲设为 x
        x.left = y.right;
        if (y.right != null) {
            y.right.parent = x;
        }
        // 将 x 的父亲设为 y 的父亲，并更新 y 的父亲的相应孩子指针
        y.parent = x.parent;
        if (x.parent == null) { // 如果 x 是根节点，那么将 y 设为新的根节点
            this.root = y;
        } else if (x == x.parent.right) { // 如果 x 是其父节点的右孩子，那么将 y 设为其父节点的右孩子
            x.parent.right = y;
        } else { // 如果 x 是其父节点的左孩子，那么将 y 设为其父节点的左孩子
            x.parent.left = y;
        }
        // 将 y 的右孩子设为 x，并将 x 的父亲设为 y
        y.right = x;
        x.parent = y;
    }

    // 辅助方法，用 v 节点替换 u 节点
    public void transplant(Node u, Node v) {
        if (u.parent == null) { // 如果 u 是根节点，那么将 v 设为新的根节点
            this.root = v;
        } else if (u == u.parent.left) { // 如果 u 是其父节点的左孩子，那么将 v 设为其父节点的左孩子
            u.parent.left = v;
        } else { // 如果 u 是其父节点的右孩子，那么将 v 设为其父节点的右孩子
            u.parent.right = v;
        }
        if (v != null) { // 如果 v 不是 null，那么将 v 的父亲设为 u 的父亲
            v.parent = u.parent;
        }
    }

    // 辅助方法，返回以某个节点为根的子树中最小键值的节点
    public Node minimum(Node x) {
        while (x.left != null) { // 沿着左孩子指针一直向下，直到找到最左边的节点
            x = x.left;
        }
        return x;
    }

    // 辅助方法，返回以某个节点为根的子树中最大键值的节点
    public Node maximum(Node x) {
        while (x.right != null) { // 沿着右孩子指针一直向下，直到找到最右边的节点
            x = x.right;
        }
        return x;
    }

    // 辅助方法，返回树中键值等于 key 的第一个找到的节点
    public Node search(int key) {
        Node x = this.root; // 从根节点开始查找
        while (x != null && x.key != key) { // 如果 x 不是 null，并且 x 的键值不等于 key，那么继续查找
            if (key < x.key) { // 如果 key 小于 x 的键值，那么在 x 的左子树中查找
                x = x.left;
            } else { // 如果 key 大于 x 的键值，那么在 x 的右子树中查找
                x = x.right;
            }
        }
        return x; // 返回找到的节点或 null
    }

    // 向树中插入一个键值为 key 的节点
    public void insert(int key) {
        Node z = new Node(key, 1); // 创建一个新节点 z，并将其颜色设为红色
        Node y = null; // 初始化 y 为 null，用于记录 z 的父节点
        Node x = this.root; // 初始化 x 为根节点，用于查找 z 的插入位置
        while (x != null) { // 如果 x 不是 null，那么继续查找
            y = x; // 将 y 设为当前的 x 节点
            if (z.key < x.key) { // 如果 z 的键值小于 x 的键值，那么在 x 的左子树中查找
                x = x.left;
            } else { // 如果 z 的键值大于或等于 x 的键值，那么在 x 的右子树中查找
                x = x.right;
            }
        }
        z.parent = y; // 将 z 的父节点设为 y
        if (y == null) { // 如果 y 是 null，说明树是空的，那么将 z 设为根节点
            this.root = z;
        } else if (z.key < y.key) { // 如果 z 的键值小于 y 的键值，那么将 z 设为 y 的左孩子
            y.left = z;
        } else { // 如果 z 的键值大于或等于 y 的键值，那么将 z 设为 y 的右孩子
            y.right = z;
        }
        insertFixup(z); // 调用插入修复方法，恢复红黑性质
    }

   // 插入修复方法，用于恢复红黑树的性质
public void insertFixup(Node z) {
    // 当 z 的父节点存在且是红色时，需要进行调整
    while (z.parent != null && z.parent.color == Color.RED) {
        // 判断 z 的父节点是其祖父节点的左孩子还是右孩子
        if (z.parent == z.parent.parent.left) {
            // 如果是左孩子，那么获取 z 的叔叔节点（祖父节点的右孩子）
            Node y = z.parent.parent.right;
            // 根据叔叔节点的颜色分为三种情况
            if (y != null && y.color == Color.RED) {
                // 如果叔叔节点是红色，那么将父节点和叔叔节点都变为黑色，将祖父节点变为红色，并将祖父节点作为新的 z 节点，继续向上调整
                z.parent.color = Color.BLACK;
                y.color = Color.BLACK;
                z.parent.parent.color = Color.RED;
                z = z.parent.parent;
            } else {
                // 如果叔叔节点是黑色或 NIL，那么需要进行旋转操作
                if (z == z.parent.right) {
                    // 如果 z 是其父节点的右孩子，那么先对父节点进行左旋，然后交换 z 和其父节点的角色
                    z = z.parent;
                    leftRotate(z);
                }
                // 如果 z 是其父节点的左孩子，那么对祖父节点进行右旋，然后将父节点变为黑色，将祖父节点变为红色，并结束调整
                z.parent.color = Color.BLACK;
                z.parent.parent.color = Color.RED;
                rightRotate(z.parent.parent);
            }
        } else {
            // 如果是右孩子，那么获取 z 的叔叔节点（祖父节点的左孩子），与上面类似，只是左右对称
            Node y = z.parent.parent.left;
            // 根据叔叔节点的颜色分为三种情况
            if (y != null && y.color == Color.RED) {
                // 如果叔叔节点是红色，那么将父节点和叔叔节点都变为黑色，将祖父节点变为红色，并将祖父节点作为新的 z 节点，继续向上调整
                z.parent.color = Color.BLACK;
                y.color = Color.BLACK;
                z.parent.parent.color = Color.RED;
                z = z.parent.parent;
            } else {
                // 如果叔叔节点是黑色或 NIL，那么需要进行旋转操作
                if (z == z.parent.left) {
                    // 如果 z 是其父节点的左孩子，那么先对父节点进行右旋，然后交换 z 和其父节点的角色
                    z = z.parent;
                    rightRotate(z);
                }
                // 如果 z 是其父节点的右孩子，那么对祖父节点进行左旋，然后将父节点变为黑色，将祖父节点变为红色，并结束调整
                z.parent.color = Color.BLACK;
                z.parent.parent.color = Color.RED;
                leftRotate(z.parent.parent);
            }
        }
    }
    // 最后确保根节点是黑色
    this.root.color = Color.BLACK;
}

// 从树中删除一个键值为 key 的节点
public void delete(int key) {
    Node z = search(key); // 查找要删除的节点
    if (z == null) { // 如果没有找到，直接返回
        return;
    }
    Node x; // 用于记录替换后的新节点
    Node y = z; // 用于记录要删除或移动的原始节点
    Color yOriginalColor = y.color; // 用于记录 y 的原始颜色
    if (z.left == null) { // 如果 z 没有左孩子，那么用其右孩子替换它
        x = z.right;
        transplant(z, z.right);
    } else if (z.right == null) { // 如果 z 没有右孩子，那么用其左孩子替换它
        x = z.left;
        transplant(z, z.left);
    } else { // 如果 z 有两个孩子，那么用其后继节点（右子树中最小的节点）替换它
        y = minimum(z.right); // 找到 z 的后继节点
        yOriginalColor = y.color; // 记录 y 的原始颜色
        x = y.right; // 记录 y 的右孩子
        if (y.parent == z) { // 如果 y 是 z 的右孩子，那么直接将 x 的父亲设为 y
            x.parent = y;
        } else { // 如果 y 不是 z 的右孩子，那么用 x 替换 y，并将 y 的右孩子设为 z 的右孩子
            transplant(y, y.right);
            y.right = z.right;
            y.right.parent = y;
        }
        transplant(z, y); // 用 y 替换 z，并将 y 的左孩子设为 z 的左孩子
        y.left = z.left;
        y.left.parent = y;
        y.color = z.color; // 将 y 的颜色设为 z 的颜色
    }
    if (yOriginalColor == Color.BLACK) { // 如果 y 的原始颜色是黑色，那么就存在过度黑问题，需要调用删除修复方法，恢复红黑性质
        deleteFixup(x);
    }
}
  
  // 删除修复方法，用于恢复红黑性质
public void deleteFixup(Node x) {
    // 当 x 不是根节点，并且是黑色时，需要进行调整
    while (x != this.root && x.color == Color.BLACK) {
        // 判断 x 是其父节点的左孩子还是右孩子
        if (x == x.parent.left) {
            // 如果是左孩子，那么获取 x 的兄弟节点（父节点的右孩子）
            Node w = x.parent.right;
            // 根据兄弟节点的颜色分为四种情况
            if (w.color == Color.RED) {
                // 如果兄弟节点是红色，那么将兄弟节点变为黑色，将父节点变为红色，并对父节点进行左旋，然后更新兄弟节点
                w.color = Color.BLACK;
                x.parent.color = Color.RED;
                leftRotate(x.parent);
                w = x.parent.right;
            }
            if (w.left.color == Color.BLACK && w.right.color == Color.BLACK) {
                // 如果兄弟节点的两个孩子都是黑色或 NIL，那么将兄弟节点变为红色，并将父节点作为新的 x 节点，继续向上调整
                w.color = Color.RED;
                x = x.parent;
            } else {
                // 如果兄弟节点的两个孩子不都是黑色或 NIL，那么需要进行旋转操作
                if (w.right.color == Color.BLACK) {
                    // 如果兄弟节点的右孩子是黑色或 NIL，那么将兄弟节点变为红色，将兄弟节点的左孩子变为黑色，并对兄弟节点进行右旋，然后更新兄弟节点
                    w.color = Color.RED;
                    w.left.color = Color.BLACK;
                    rightRotate(w);
                    w = x.parent.right;
                }
                // 如果兄弟节点的右孩子是红色，那么将父节点的颜色赋给兄弟节点，将父节点和兄弟节点的右孩子都变为黑色，并对父节点进行左旋，然后结束调整
                w.color = x.parent.color;
                x.parent.color = Color.BLACK;
                w.right.color = Color.BLACK;
                leftRotate(x.parent);
                x = this.root; // 将 x 设为根节点，结束循环
            }
        } else {
            // 如果是右孩子，那么获取 x 的兄弟节点（父节点的左孩子），与上面类似，只是左右对称
            Node w = x.parent.left;
            // 根据兄弟节点的颜色分为四种情况
            if (w.color == Color.RED) {
                // 如果兄弟节点是红色，那么将兄弟节点变为黑色，将父节点变为红色，并对父节点进行右旋，然后更新兄弟节点
                w.color = Color.BLACK;
                x.parent.color = Color.RED;
                rightRotate(x.parent);
                w = x.parent.left;
            }
            if (w.right.color == Color.BLACK && w.left.color == Color.BLACK) {
                // 如果兄弟节点的两个孩子都是黑色或 NIL，那么将兄弟节点变为红色，并将父节点作为新的 x 节点，继续向上调整
                w.color = Color.RED;
                x = x.parent;
            } else {
                // 如果兄弟节点的两个孩子不都是黑色或 NIL，那么需要进行旋转操作
                if (w.left.color == Color.BLACK) {
                    // 如果兄弟节点的左孩子是黑色或 NIL，那么将兄弟节点变为红色，将兄弟节点的右孩子变为黑色，并对兄弟节点进行左旋，然后更新兄弟节点
                    w.color = Color.RED;
                    w.right.color = Color.BLACK;
                    leftRotate(w);
                    w = x.parent.left;
                }
                // 如果兄弟节点的左孩子是红色，那么将父节点的颜色赋给兄弟节点，将父节点和兄弟节点的左孩子都变为黑色，并对父节点进行右旋，然后结束调整
                w.color = x.parent.color;
                x.parent.color = Color.BLACK;
                w.left.color = Color.BLACK;
                rightRotate(x.parent);
                x = this.root; // 将 x 设为根节点，结束循环
            }
        }
    }
    // 最后确保根节点是黑色
    this.root.color = Color.BLACK;
}