引言
树是一种重要的数据结构，而二叉搜索树（BST）则是树的一种常见形式。在本文中，我们将学习如何构建一个高效的二叉搜索树联系簿，以便快速插入、搜索和删除联系人信息。

介绍二叉搜索树

二叉搜索树是一种有序的二叉树，其中每个节点都包含一个可比较的键和关联的值。它满足以下性质：
1.左子树中的所有节点的键值小于当前节点的键值。
2.右子树中的所有节点的键值大于当前节点的键值。

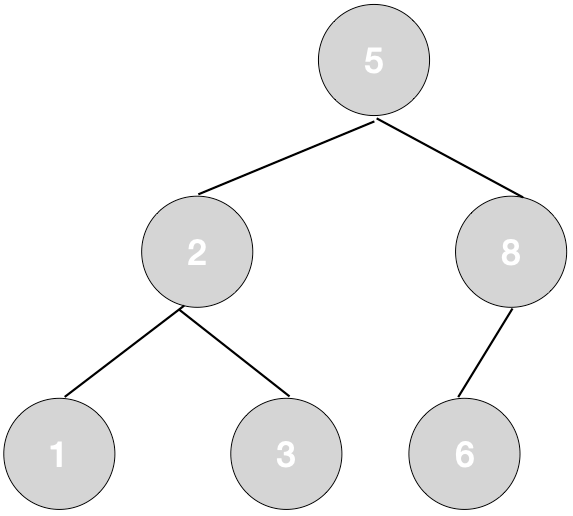
3.没有重复的节点。

二叉搜索树的结构使得在其中插入、搜索和删除节点的操作都能在平均时间复杂度为O(log n)的情况下完成。

构建联系簿结构
我们将使用Go语言来实现这个联系簿结构。首先，我们定义一个AddressBookNode结构体，它代表树中的一个节点，并包含姓名、联系信息以及左右子节点的指针。

type AddressBookNode struct {
    Name         string
    ContactInfo  string
    Left         *AddressBookNode
    Right        *AddressBookNode
}

插入联系人
为了将联系人添加到联系簿中，我们实现了InsertContact方法。该方法接受一个姓名和联系信息作为输入，并根据二叉搜索树的性质将联系人插入到合适的位置。

func (n *AddressBookNode) InsertContact(name, contactInfo string) *AddressBookNode {
    if n == nil {
        return &AddressBookNode{Name: name, ContactInfo: contactInfo, Left: nil, Right: nil}
    }

    if name < n.Name {
        n.Left = n.Left.InsertContact(name, contactInfo)
    } else if name > n.Name {
        n.Right = n.Right.InsertContact(name, contactInfo)
    }

    return n
}

该方法的工作原理如下：
1.如果当前节点为空，则树为空，我们将使用提供的姓名和联系信息创建一个新的AddressBookNode，并将其作为树的根节点。
2.如果当前节点不为空，则将新联系人的姓名与当前节点的姓名进行比较：
  2.1如果新姓名小于当前节点的姓名，则在左子树上递归调用InsertContact方法。
  2.2如果新姓名大于当前节点的姓名，则在右子树上递归调用InsertContact方法。
  2.3如果新姓名等于当前节点的姓名，则可以根据实际需求进行处理（例如，更新联系信息）。

3.返回修改后的节点。请注意，尽管在递归调用期间可能会修改树的结构，但根节点保持不变，并且返回修改后的树。

搜索联系人
为了在联系簿中搜索联系人，我们实现了SearchContact方法。该方法接受一个姓名作为输入，并在二叉搜索树中递归搜索匹配的联系人。

func (n *AddressBookNode) SearchContact(name string) (string, bool) {
    if n == nil {
        return "", false
    }

    if name == n.Name {
        return n.ContactInfo, true
    }

    if name < n.Name {
        return n.Left.SearchContact(name)
    }
    return n.Right.SearchContact(name)
}

该方法的工作原理如下：
1.如果当前节点为空，则表示在树中没有找到指定姓名的联系人，此时方法返回一个空字符串和false。
2.如果目标姓名小于当前节点的姓名，则在左子树上递归调用SearchContact方法。
3.如果目标姓名大于当前节点的姓名，则在右子树上递归调用SearchContact方法。

4.如果目标姓名与当前节点的姓名相等，则表示找到了要搜索的联系人节点。方法返回该节点的联系信息和true。

删除联系人
为了从联系簿中删除联系人，我们实现了DeleteContact方法。该方法接受一个姓名作为输入，并在二叉搜索树中递归删除匹配的联系人。

func (n *AddressBookNode) DeleteContact(name string) *AddressBookNode {
    if n == nil {
        return nil
    }

    if name < n.Name {
        n.Left = n.Left.DeleteContact(name)
    } else if name > n.Name {
        n.Right = n.Right.DeleteContact(name)
    } else {
        if n.Left == nil && n.Right == nil {
            return nil
        } else if n.Left == nil {
            return n.Right
        } else if n.Right == nil {
            return n.Left
        }

        minNode := n.Right.FindMin()
        n.Name = minNode.Name
        n.ContactInfo = minNode.ContactInfo
        n.Right = n.Right.DeleteContact(minNode.Name)
    }

    return n
}

该方法的工作原理如下：
1.如果当前节点为空，则表示在树中没有找到指定姓名的联系人，此时方法返回nil。
2.如果目标姓名小于当前节点的姓名，则在左子树上递归调用DeleteContact方法。
3.如果目标姓名大于当前节点的姓名，则在右子树上递归调用DeleteContact方法。
4.如果目标姓名与当前节点的姓名相等，则需要根据节点的情况进行删除操作：
  4.1如果目标节点是叶子节点（没有子节点），直接将其设置为nil。
  4.2如果目标节点只有一个子节点（左子树或右子树），将其子节点替代目标节点的位置。

  4.3如果目标节点有两个子节点，则找到右子树中的最小节点，将其值复制到目标节点，并递归删除最小节点。

总结
通过构建高效的二叉搜索树联系簿，我们可以轻松地插入、搜索和删除联系人信息。使用适当的算法和数据结构，我们能够在O(log n)的时间复杂度内执行这些操作。这对于需要频繁处理联系人信息的应用程序来说尤为重要。