大模型这个“数字巨兽”，吞噬着海量内存和算力，让你的笔记本电脑瑟瑟发抖。以LLaMA-70B为例，在常规的FP16精度下，它需要高达140GB的内存空间，几乎所有的消费级GPU都只能“望洋兴叹”。随着模型参数从百亿卷到千亿，甚至万亿，这个挑战变得愈发尖锐。于是“量化”技术临危受命，被推上了历史舞台。

如果能把模型从16位浮点数，压缩到2-4位的整数，就能实现4到8倍的惊人压缩比，内存占用和计算开销都能显著下降。但进行2位这种“骨感”量化时，一个巨大的拦路虎出现了：灾难性的性能雪崩。罪魁祸首，正是在激活值中潜藏的那些“异常值”（outliers）。这些家伙就像班级里特别调皮捣蛋的学生，占据了动态范围的大部分，让低位量化这个“脸盲”老师根本无法准确识别出模型的真实意图。正如Sun等人所指出的，异常值问题，就是卡在低位压缩咽喉里的一根鱼刺，亟需一场技术革新来将其拔除。

一刀切的“旋转术”为何走入死胡同
面对“异常值”，前人们并非束手无策。能不能在量化前，先给它们做个“微整形”，把棱角磨平？这就是基于旋转的量化方法，核心理论叫做“计算不变性”（computational invariance）。QuIP（非相干性处理量化）和QuaRot（量化旋转）就是这个流派的杰出代表。QuIP选择使用随机的正交矩阵，有点像随缘“整容”；而QuaRot则采用了大名鼎鼎的Hadamard（阿达玛）变换，这是一种结构非常规整、理论性质优美的变换。

它们通过这种旋转操作，成功地将激活值重新分布，有效地“稀释”了那些扎眼的异常特征，同时又没有改变模型每一层的数学本质。这些方法虽然取得了阶段性的成功，却共享着一个致命的局限：它们使用的变换矩阵是固定的、与数据无关的，无法通过梯度下降这种深度学习的“灵魂”来进行优化和调整。这种“一刀切”的策略，给所有不同特点的层都用同一套“整形方案”，这与大语言模型内在的复杂性产生了根本性的冲突，因为LLM在不同层之间表现出了显著的“异质性”。

Transformer模型中的不同层，面临着截然不同的量化挑战，各有各的“脾气”：

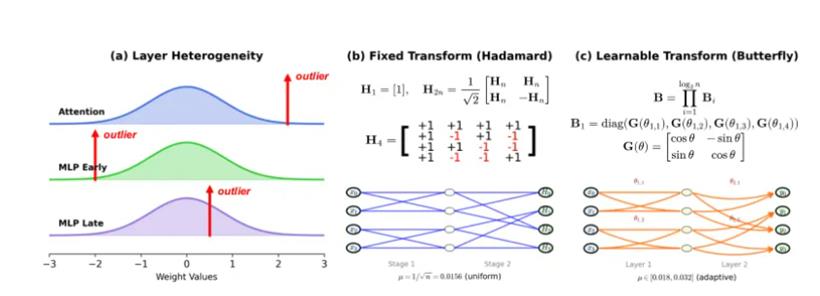
注意力层（attention layers）因为softmax（柔性最大值传输函数）操作的天然属性，异常值往往集中在分布的正尾部，像个“右撇子”。早期的MLP（多层感知器）层，由于SwiGLU（Swish门控线性单元）这类门控函数的影响，又常常在负区域“秀肌肉”，表现出不对称的负激活，是个“左撇子”。而到了更深层的晚期MLP（多层感知器）层，数值伪影（numerical artifacts）开始在分布的两端边界累积，异常值像“双峰骆驼”一样出现在边界附近。

这种千差万别的模式源于每一层在庞大模型架构中扮演的角色不同。既然病症各异，又怎能用一副“万金油”式的固定旋转来包治百病呢？特别是QuaRot所倚重的Hadamard变换，它虽然在理论上达到了最优的最坏情况相干性，意味着它在“信息打散”方面做得最均匀，但它的矩阵元素是由离散的{+1, -1}构成的。这种离散的特性，就像一块坚硬的水晶，结构完美但无法被雕琢，使其无法通过基于梯度的优化来适应每一层的具体情况，只能被迫采用“一刀切”的通用疗法。这种方法面对Transformer层中千奇百怪的异常值模式时，就显得力不从心了。

蝴蝶展翅：一场优雅的可学习革命
为了打破固定变换的枷锁，研究者们提出了一个全新的、充满想象力的解决方案：ButterflyQuant。它的核心思想，就是用一种新颖的、可学习的“蝴蝶变换”（Butterfly Transform）来取代固定的Hadamard旋转。ButterflyQuant的真正创新之处，在于它放弃了Hadamard变换那种由离散的{+1, -1}构成的“刚性骨架”，转而采用由连续的Givens（吉文斯）旋转角度来参数化。这种连续的参数化，使得变换矩阵可以通过梯度下降进行平滑、精细的优化，就像给这块“水晶”注入了生命，让它可以根据需求自由变形。同时，其精巧的数学构造又保证了无论怎么“变形”，它始终是一个完美的正交矩阵，不会破坏“计算不变性”这个根本法则。

ButterflyQuant的洞见是革命性的：它深刻认识到，不同的Transformer层展现出迥异的异常值模式，需要的不是一种通用的旋转方案，而是一种能够为每一层“量身定制”的自适应旋转。通过为模型中的每一层学习其独特的旋转模式，ButterflyQuant能够更精准地应对五花八门的异常值分布，从而在极端的低位量化（比如2位）下，实现前所未有的性能。

更妙的是，蝴蝶变换与Hadamard变换之间还有着深刻的血缘关系。对于n=2ᵏ的维度，Hadamard矩阵Hₙ可以被精确地表示为一个选择了特定角度参数的蝴蝶变换。这说明，Hadamard变换只是蝴蝶变换参数空间中的一个特例。蝴蝶变换是一个更广阔、更灵活的框架，它包含了前者，表达能力远超前者。

当然，蝴蝶变换的递归结构天然偏爱2的幂次方的维度（如128、1024、4096）。但许多现实中的大模型，其隐藏层维度并非如此规整，比如LLaMA-2-13B的维度是5120。为了解决这个“尺寸不合”的问题，ButterflyQuant巧妙地引入了基于Kronecker（克罗内克）积的复合变换。

严谨的训练与惊艳的成果
为了让蝴蝶变换学会如何“对症下药”，研究者们设计了一个精巧的损失函数。它由两部分组成：一部分是“重建损失”，目标是让量化后的模型输出与原始模型输出尽可能接近，这是保证性能的基本盘。另一部分是“均匀性正则化”，它通过计算旋转后激活值的分布与均匀分布之间的KL（吉布斯）散度，来鼓励变换将激活值均匀地分布到各个量化区间里。

这种做法基于一个深刻的信息论原理：对于给定的位宽，均匀分布能够实现熵的最大化，从而最大程度地保留信息。最终的实验结果，可以说是对ButterflyQuant强大能力的最有力证明。在对LLaMA-2-7B和LLaMA-2-13B模型进行的严苛的2位权重量化（W2A16）测试中，ButterflyQuant的表现堪称降维打击。

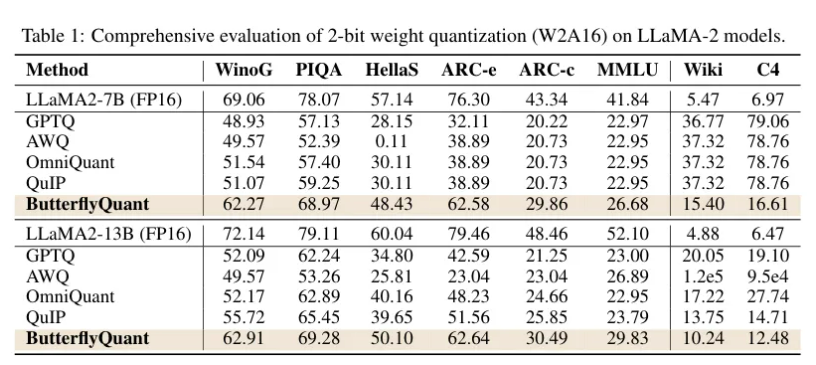
从表中可以看到，在衡量语言模型基础能力的困惑度指标上，ButterflyQuant取得了压倒性胜利。在WikiText-2数据集上，7B模型的困惑度仅为15.40，而表现最好的基线方法GPTQ（生成式预训练变换器量化）高达36.77，差距悬殊。在13B模型上，它更是以10.24的困惑度远低于QuIP的13.75。值得注意的是，像AWQ（激活感知权重量化）这样的方法，在13B模型上困惑度直接“爆表”，超过了10万，这说明在极端低位量化下，传统的异常值处理方法已经彻底失效。而在多个零样本推理任务上，ButterflyQuant平均保留了FP16基准88%的准确率，而其他方法只能保留65-73%。这种在不同模型规模、不同评测任务上的一致性优势，强有力地证明了其层自适应方法的普适性和有效性。

这只“蝴蝶”将飞向何方
ButterflyQuant的问世，为在消费级硬件上部署真正强大的大语言模型，推开了一扇尘封已久的大门。通过高效的2位量化，它能将LLaMA-2-7B模型从14GB，压缩到仅1.75GB，使其能够在普通笔记本电脑，甚至智能手机上流畅运行。在边缘计算领域，ButterflyQuant的低内存占用和计算需求，使得模型可以直接在本地设备上运行，无需将可能包含隐私的数据上传到云端。这不仅大大降低了网络延迟，更从根本上保障了数据的隐私和安全。

对于云服务提供商而言，内存和计算资源是其运营成本的核心。ButterflyQuant的超高压缩比，意味着服务商可以在相同的硬件上承载更多的用户请求，或使用更廉价的硬件来提供同等质量的服务，从而有效降低“模型即服务”（MaaS）的成本。这只优雅的“蝴蝶”，给大模型插上了最美丽的翅膀。

参考文献
https://arxiv.org/abs/2509.09679
https://arxiv.org/abs/2404.00456
https://arxiv.org/abs/2306.12929
https://arxiv.org/abs/2307.13304
https://arxiv.org/abs/2407.11062
https://arxiv.org/abs/2502.13178